Tractography

     The advent of diffusion weighted magnetic resonance imaging has provided the opportunity for non-invasive investigation of neural architecture. Using this imaging technique, neuroscientists can determine how neurons originating from one region connect to other regions and how well-defined those connections may be. For such studies, the quality of the results relies heavily on the chosen fiber representation and the method of reconstructing pathways.

     To begin studying the microstructure of fibers, we need a model to interpret the diffusion weighted signal. Such models fall broadly into two categories: parametric and nonparametric. Based on these models, several techniques attempt to reconstruct pathways. Deterministic tractography involves directly following the diffusion pathways. In the single tensor model, this means simply following the principal diffusion direction, while multi-fiber models often include techniques for determining the 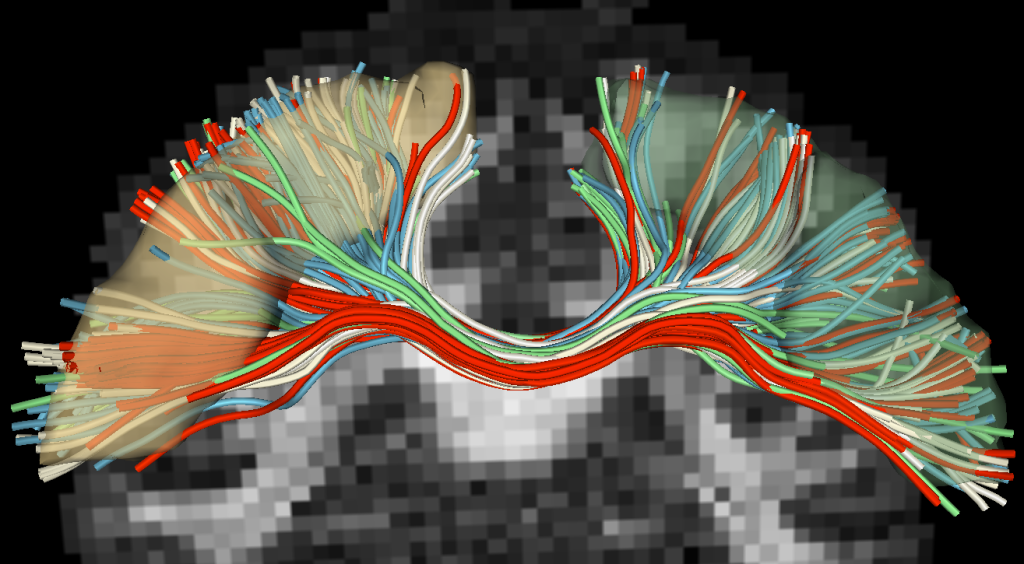number of fibers present or when pathways branch.

      Most tractography approaches fit the model at each voxel independent of other voxels; however, tractography is a causal process: we arrive at each new position along the fiber based upon the diffusion found at the previous position. Here, we treat model estimation and tractography as such by placing this process within a causal filter. As we examine the signal at each new position, the filter recursively updates the underlying local model parameters, provides the variance of that estimate, and indicates the direction in which to propagate tractography.

      To begin estimating within a finite dimensional filter, we model the diffusion signal using a mixture of either two or three Gaussian tensors. This enables estimation directly from the raw signal data without separate preprocessing or regularization steps. Because the signal reconstruction is nonlinear, we use the unscented Kalman filter to estimate the model parameters and then propagate in the most consistent direction. Using causal estimation in this way yields inherent path regularization and accurate fiber resolution at crossing angles not found with independent optimization. We further note that the approach presented here generalizes to arbitrary fiber model with finite dimensional parameter space.

     This tractography algorithm is very robust and was one of the winners of the FiberCup competition held at MICCAI in 2009. More details about this tractography algorithm may be found in the hyperlinked presentation and paper. Below is a video that shows tractography of the corticospinal tract (yellow) and the corpus callosum (red) using the two-tensor model.

 Visualizing White Matter