Free Water

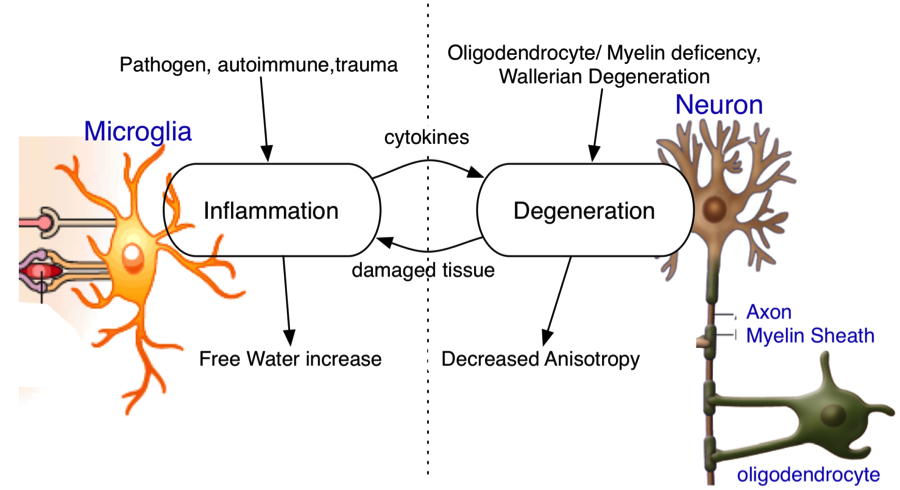
     Free-water imaging is an analysis method for diffusion MRI data, which separately models the contribution of extracellular free water and water that is in the vicinity of cellular tissue. Using free-water imaging increases the precision of conventional metrics such as FA and Trace, and quantitatively estimates the degree of vasogenic edema and also likely neuroinflammation. Correcting for free water removes partial volume effects and increases precision of fiber tractography through regions affected by CSF contamination, and edema. Being able to separate extracellular free water from water in the tissue means that group differences can be evaluated for abnormalities in the extracellular space, such as neuroinflammation, and for tissue abnormalities such as axonal degeneration. This is important since extracellular and cellular processes such as neuroinflammation and axonal degeneration have similar effects of conventional diffusion MRI measures, such as those derived from diffusion tensor imaging (DTI).  Identifying between the two types of pathologies is important since it help us understand the source of the disorder, as well as plan treatment strategies that can target a specific pathology. Specifically we believe that in many disorders chronic neuroinflammation preceeds and may cause eventual cellular degeneration.

        Using free-water imaging we were able to demonstrate extracellular abnormalities in first episode schizophrenia. We were also able to identify microstructural abnormalities in players suffering from concussions, subjects with mild cognitive impairment that will develop Alzheimer’s disease and in normal aging. We are currently studying the model in many other types of neurodegenerative disorders.

     Free-water is defined as self-diffusing water molecules that do not experience restriction or hindrance from their surrounding. This definition depends on the amount of time in which the diffusion process is measured, as for infinitely long diffusion times, all water molecules will eventually hit an obstacle, whereas for infinitely short diffusion time, all water molecules are free to diffuse. In typical experimental setups the diffusion time is in the order of 30-50ms which yields that in order for water molecules to diffuse freely they have to be a few tens of microns away from membranes and other cellular restrictions. The typical size of brain cells is usually lower than 10 microns, and therefore in the brain, free-water can be found in the extra-cellular space. The diffusion coefficient of free-water is known, and depends on the temperature. For example, the diffusion coefficient of water in body temperature is d =3×10−3 mm2/s .

     The model assumes that the diffusion signal originates from two molecular compartments, co-existing within a voxel, with slow exchange between the compartments. The first compartment is a tissue compartment, modeled by a diffusion tensor. The second compartment is an isotropic compartment, with a fixed diffusion coefficient, d, set to the diffusion coefficient of water in body temperature, 3 × 10−3 mm2 /s. Thus, the isotropic compartment models free-water, and is expected to measure molecules that are in the extracellular space, we call this compartment the free-water compartment. If the free-water compartment is eliminated, then the remaining compartment measures molecules that are close to tissue membranes, these are expected to include all the intracellular molecules, and some of the extracellular molecules that are not far enough from hindering obstacles such as cellular membranes.

     The free water model estimates free-water maps, which are the fractional volume of the free-water compartment. The model also yields diffusion tensors that are corrected for the contribution of free-water. From these tensors we can extract DTI maps such as, FA, mean diffusivity, axial and radial diffusivities. Since these parameters model the tissue compartment we term them tissue FA (FAt), tissue mean diffusivity (MDt), etc.